A Link Between Twistors, Spirals and Light?

If you mix turning with going forward, you get a spiral. Kids draw them before they can write. Ancient carvers in Ireland, Wales, and Polynesia cut them into stone and bone.

The shape feels like motion captured—and for some peculiar reason, ancient peoples all seemed to capture this form in their artwork (O’Kelly 1982; Lynch 1991). Ezekiel described something similar with his “wheel within a wheel.” He said the wheels could go in any direction without turning, which is a strange way to talk about a wheel unless you’re trying to describe movement that isn’t confined to one axis—much like a twistor. That’s exactly how it sounds: coupled rotations that can move without reorienting first (NRSV 2010, Ezek. 1:16).

Twentieth‑century physics found its own version of this shape in light. In twistor theory, a single light ray—what relativity calls a null geodesic—isn’t just a path; it’s a point in another space, twistor space. Flip the mapping around and a single spacetime event becomes a whole sphere of light rays through it. Light, in this picture, organizes the world as families of linked circles and lines; you study physics by following those families instead of points marching through time (Penrose and Rindler 1984; Ward and Wells 1990; Penrose 2009).

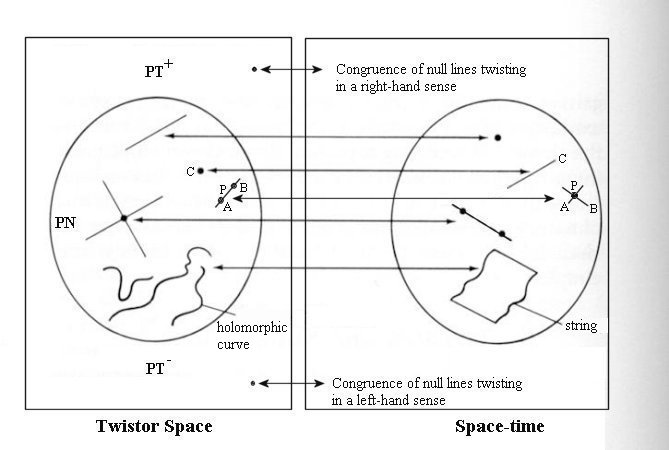
This way of looking at things is powerful because it encodes motion and orientation at once. The algebra that pairs a twistor with a spacetime point—the incidence relation—says, in effect, “this ray passes through this event.” It’s a compact way of keeping track of how light threads the world (Penrose and Rindler 1984; Ward and Wells 1990).

There’s another way the spiral and the ray meet, if you’ll allow a bolder leap. If a person is, in some deep sense, a holomorphic projection—an ethereal being of light braided to the energy of their surroundings—then what we call “truth” is the coherence of that projection. The information‑energy that modulates the incoming wave (what really happened around us) is collapsed, through a holomorphic process, into the particles of our being. It seeds the “golden crystals” of DNA—the slow spiral in our cells—with pattern and memory: the trace of our days, and echoes of our ancestors. Life works when the projection is faithful; distortions of truth scramble the pattern and fray our health. And if consciousness is the capacity to reflect upon the information that one is, and that information is replicated in every strand, it is not unreasonable to imagine consciousness able to unbind from the body and continue its process (St. John 2018).

What does any of this have to do with spirals on stones? More than it seems. A spiral is what you get when two simple symmetries cooperate: rotation and scaling. Turn by a fixed angle, grow by a fixed factor, repeat. Physics leans on the same lesson: structures that matter most often emerge from symmetries. Light’s paths are special because they sit right on the boundary set by the speed of light; that boundary—the light cone—becomes fundamental in twistor theory. Build geometry out of those boundaries and you meet patterns that look like interlocked circles and twisted families of lines—mathematically tidy cousins of “a wheel within a wheel” (Wald 1984; Penrose 2009).

Physicists even talk about helicity—spin along the direction a massless particle moves—which is another way of saying the state is part rotation, part translation. In twistor language, the representation of these massless states is built into the geometry, not added afterward. Hence it feels natural, in this picture, that light comes in “right‑spinning” and “left‑spinning” versions, handled cleanly by the same map that turns rays into points and points into spheres (Peskin and Schroeder 1995; Ward and Wells 1990).

If you zoom back out, you notice the same trick appearing in old stories. One Irish tale says a carved five‑coil spiral with a line through it acts like a magnet between worlds: bring the coils close and the two realms touch (O’Kelly 1982). As metaphors go, that’s remarkably close to what the twistor map does: it lets you pass between two descriptions of the same thing—events and rays—by following a simple rule (Penrose and Rindler 1984).

Of course the carvers of Newgrange or the artists who paint the Māori koru weren’t writing twistor equations. But they were noticing the same kind of structure: flows that preserve form while changing scale, and motions that combine turning with going somewhere (O’Kelly 1982; Mead 1984). If you want to show contact between layers of reality—earth and sky, human and divine—it’s hard to beat a spiral or “wheels within wheels.”

A useful rule of thumb is that whenever you see a shape recur across time and fields, there’s probably an invariance hiding underneath. Spirals are what happens when rotation meets scale. Ezekiel’s wheels are what you get when you try to describe coupled motion without reorientation. Twistor theory is what you get when you build physics out of the invariance of light’s direction. And if our lives are holomorphic projections, then health is coherence in that projection, and insight comes from attending to the light‑thread that runs through it all (St. John 2018). Different languages, same grammar.

References

• Lynch, Frances. Prehistoric Anglesey: The Archaeology of the Island to the Roman Conquest. Rev. ed. Stroud: Sutton Publishing, 1991.
• Mead, Sidney Moko. Te Toi Whakairo: The Art of Māori Carving. Auckland: Reed, 1984.
• New Revised Standard Version. The New Oxford Annotated Bible with the Apocrypha. 4th ed. Oxford: Oxford University Press, 2010.
• O’Kelly, Michael J. Newgrange: Archaeology, Art and Legend. London: Thames & Hudson, 1982.
• Penrose, Roger. “Twistor Theory.” Scholarpedia 4, no. 11 (2009): 7127.
• Penrose, Roger, and Wolfgang Rindler. Spinors and Space‑Time. Vol. 1: Two‑Spinor Calculus and Relativistic Fields. Cambridge: Cambridge University Press, 1984.
• Peskin, Michael E., and Daniel V. Schroeder. An Introduction to Quantum Field Theory. Boulder: Westview Press, 1995.
• St. John, Theodore J. “The Holomorphic Process: Understanding the Holographic Nature of Reality as a Metamorphic Process.” Unpublished manuscript, 2018. - https://holomorphicprocess.com/
• Wald, Robert M. General Relativity. Chicago: University of Chicago Press, 1984.
• Ward, R. S., and Raymond O. Wells, Jr. Twistor Geometry and Field Theory. Cambridge: Cambridge University Press, 1990.